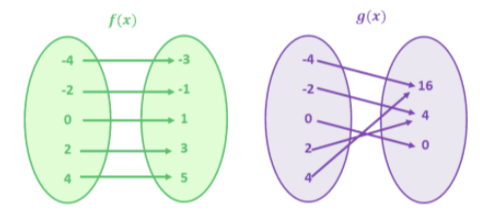
What is a function?
A function represents a calculation (or, for our purposes, computation) that uses data provided to it and the results in new data. The type of data that a function expects (i.e., the “input type”) is often called the “domain” (common in mathematics). The type of data that the function calculates (i.e., the “output type”) is often called the “codomain”.
So a function takes data from the domain and calculates data in the codomain.
Recall that one common view of computation (or computing) is the processing of data to create other data. This view aligns well with the concept of a function. A function processes data to create other data; as such, a function is a means to represent or specify computation. This perspective positions programming as the definition of multiple (likely interacting) functions.
We will refine this idea (that functions map inputs to outputs) this module, but for now will leverage our intuition and/or prior experience.
Some early function examples
Recall some of the problems that we have already thought about in our discussion of data. The webpage in the following image includes the use of (or is produced through the use of) a variety of functions. Can you list some?
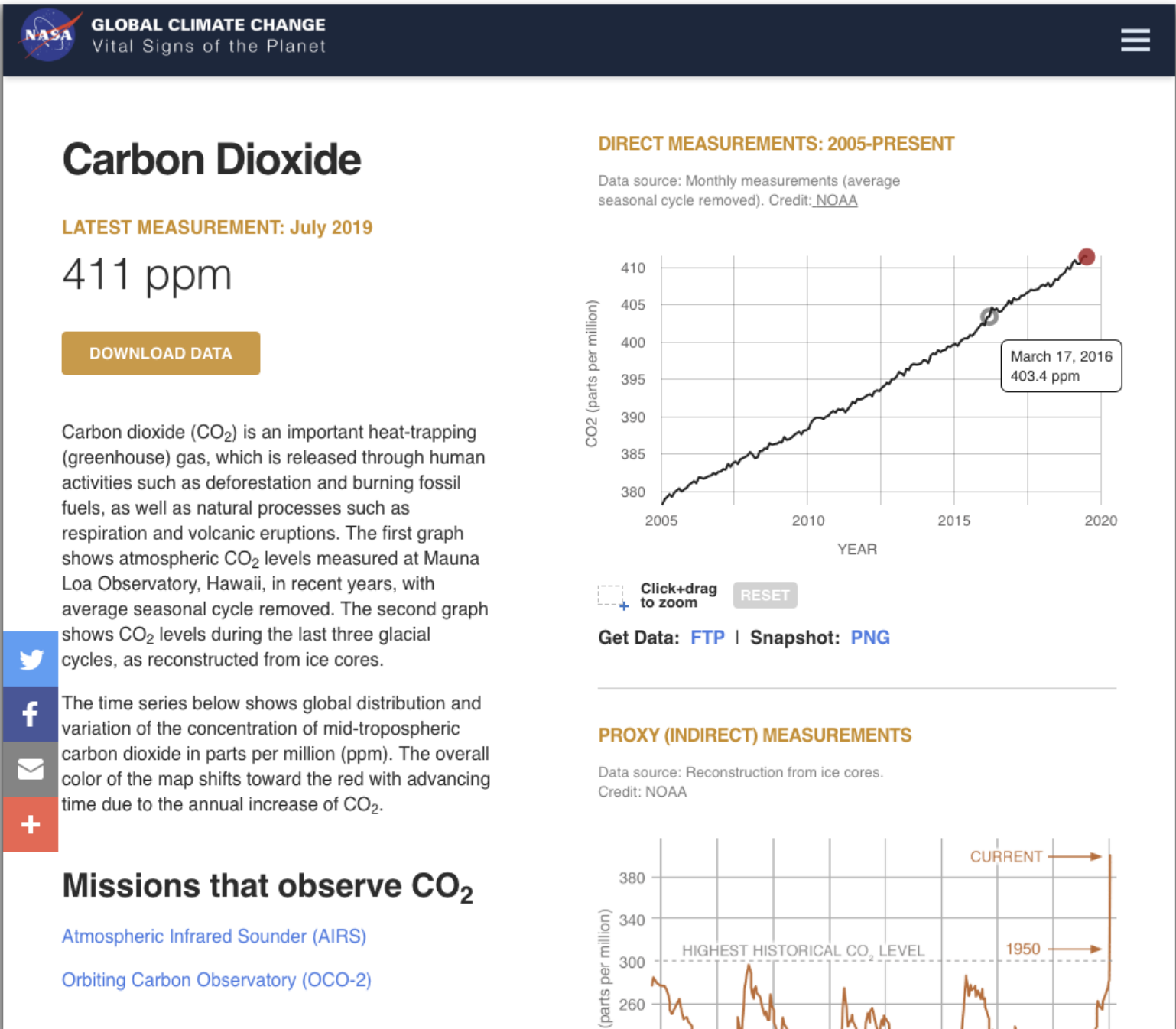
Some of the functions involved are:
- A function that takes in a year and gives us a CO2 ppm measurement.
- A function that takes in CO2 data and gives us an image.
- A function that takes in some text and gives us an image.
- A function that takes in user input and gives us an updated image (though it is not obvious in this screenshot, the graph is interactive).
There are likely many functions used in the generation of a webpage such as that shown in the image below. Though we do not know the details of the implementation of the software, we can make guesses at the sort of behaviour/functionality needed.
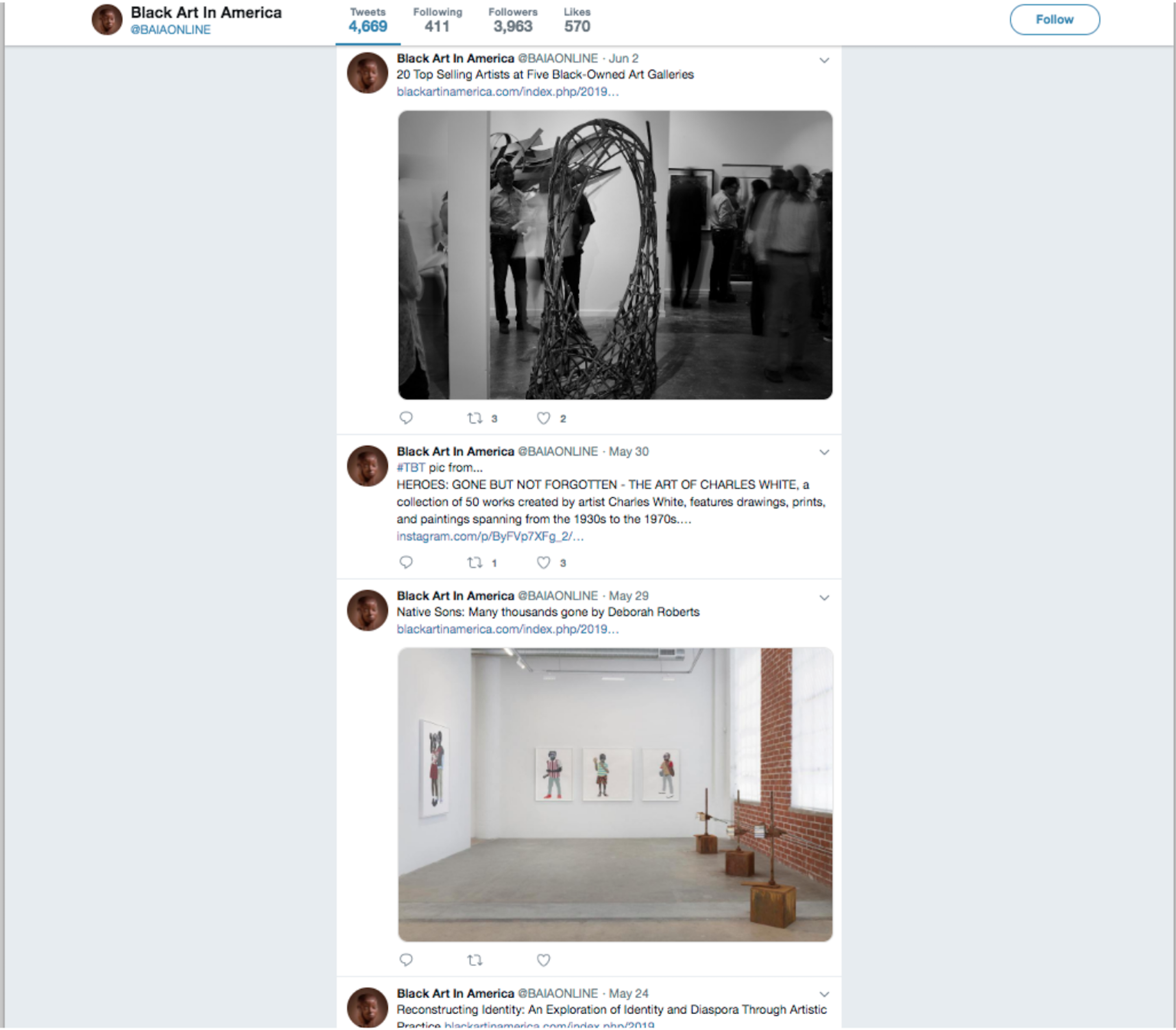
Some of the functions involved here likely include:
- A function mapping each tweet to images stored within.
- A function that maps your user credentials to “success” or “failure” when attempting to access the webpage.
- A function that maps your user id to a sequence of tweet data (what you will see).
- A function that maps your existing history and your new login time to a new history for you (so that you see new things).
How are functions represented?
You may recall the following different representations of functions from mathematics courses.
The algebraic representation
\[f(x) = x^2 + 1\]In this example, the x represents the input to the function.
When the function is applied to different values for x, you get different output values.
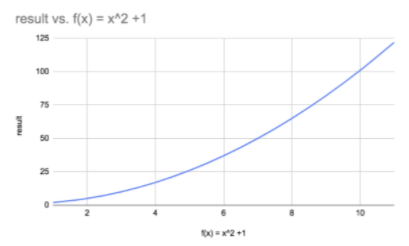
The graphical representation
Here is the function applied to increasing values of x. The input and output are plotted in the graph below.
The tabular representation
For example, applying \(f(x) = x^2 + 1\) to inputs 1 through 4.
| x | x2 + 1 |
|---|---|
| 1 | 2 |
| 2 | 5 |
| 3 | 10 |
| 4 | 17 |
Each of these representations is useful for different purposes. As relates to our goals, the algebraic representation is the only one that suggests (or declares) what the function actually does. We will explore the details of this representation and how to reason about its use during the remainder of this module (and course).
Functional decomposition
Let’s say we want to compute the area of a circle that has a diameter of 10.
What are the steps involved in solving this problem?
- We know that the area of a circle can be computed with the formula π r2, where
ris the radius of the circle. - First, we need the value of π. We know it’s roughly 3.14, but we probably want to be more precise. TypeScript lets us use
Math.PIas a drop-in for the value of π. - Then we need the radius. We can obtain the radius by halving the diameter, i.e.,
10 / 2, which gives us the value 5. - We should then square the radius, i.e.,
5 * 5.
Breaking down these steps, we get: Math.PI * (10 / 2) * (10 / 2). This can be computed using the rules for evaluating expressions that we talked about previously.
Now, suppose we have another circle of diameter 17 whose area we need to calculate.
Following the steps above, we can repeat the expression: Math.PI * (17 / 2) * (17 / 2)
One problem here is that we’re repeating ourselves. We’re defining the same strategy for computing a circle’s area from its diameter two times, and we’ll have to do it again and again any time we have a different diameter value to deal with.
To avoid this, we can use a function to encapsulate this behavior.
For example, consider the following super-simple function that simply adds 1 to the provided value.
\[f(x) = x + 1\]This mathematical function (which we’ve referred to as f) can operate on any numerical value, like 3, 45, or -10.2. That is, substituting actual numbers in place of the identifier x.
We can do the same thing for computing the area of of a circle given its diameter. But this time, instead of calling the function f, which is a pretty uninformative name, we can call it areaFromDiameter. And instead of the input variable being called x, we’ll call it d for “diameter”.
This function can be applied to any numerical value, like 10 or 17, and will give us the correct result.
Functions are abstractions
A benefit of using a function in this way is that we have now abstracted away the details of how to compute the area of a circle from its diameter. This means we can handle more complicated scenarios, like computing the area of an annulus.
An annulus is a ring made of two concentric circles. Suppose we have an annulus like below, where the outer circle has a diameter of 17, and the inner circle has a diameter of 10. If we want to compute the area of the coloured portion of this shape, what would our strategy be?
- We can compute the area of the outer circle
- Then compute the area of the inner circle
- Then compute the difference between the two areas
That is, our answer is the result of
areaFromDiameter(17) - areaFromDiameter(10)
Because we have already abstracted away the procedure for calculating the area of a single circle, we don’t have to worry about all of those little details. We can simply build on them.
This idea of functional decomposition is central to programming. We can build ever more large and complex software systems through a process of decomposing our requirements into smaller and smaller pieces and building up the system one function at a time.
Did you notice the expressions? Notice that we are performing subtraction between areaFromDiameter(17) and areaFromDiameter(10). That is, they’re being used as though they are numerical values. That’s because when the function areaFromDiameter is applied to the number 17, we get the result 226.98006922186258. The function application is an expression, because it evaluates to a value.
Functions in TypeScript
We can use this same idea of functional decomposition to write programs in TypeScript. TypeScript functions, like mathematical functions, can take inputs, perform some calculations with them, and produce a result.
Here’s what the function areaFromDiameter would look like in TypeScript.
const areaFromDiameter = (diameter: number): number => {
return Math.PI * (diameter / 2) * (diameter / 2);
}
Let’s talk about the different pieces above:
const areaFromDiameter— The function is declared usingconst. It is, after all, a named value, albeit a different kind of value than the ones we are used to, like5or"hello".(diameter: number): number— This part is called the function signature. It defines the function’s type, which is composed of the type(s) of its input(s) and the type of its output.1- The function’s inputs are also called its parameters. A function can take 0 or more parameters, and each one must have its type specified. This function takes one input, called
diameter, which is anumber. - This bit may not look like much, but at this point we’ve done a fair amount of work already! We have received our problem statement (”calculate the area of a circle given its diameter”), and we’ve expressed what a solution should look like, even if we haven’t implemented it yet.
- The function’s inputs are also called its parameters. A function can take 0 or more parameters, and each one must have its type specified. This function takes one input, called
=> { .... }— The arrow (=>) indicates that this is a function. The code inside the curly braces is the body of the function.return Math.PI * (diameter / 2) * (diameter / 2);— This is a statement that “gives back” the result of the expression, to whomever used the function.Math.PI * (diameter / 2) * (diameter / 2)is an expression. When the program executes, the entire expression will evaluate to one single value.- The
returnkeyword tells the function that that single value should be “given back” as the output.
Putting it together
Here’s that function again
const areaFromDiameter = (diameter: number): number => {
return Math.PI * (diameter / 2) * (diameter / 2);
}
We can now use this function to calculate the area of circles with any diameter.
When you use a function, you are invoking it, or calling it, or applying it. You will frequently hear the phrase “call a function”. You can call a function in TypeScript by
- typing its name, and
- within parentheses, providing input values for each of its parameters
If the function does not expect any inputs, you still need to provide empty parentheses! I.e., ()
The parentheses indicate that you are calling (or invoking, or applying) the function.
Let’s call areaFromDiameter with some input values.
areaFromDiameter(10)
areaFromDiameter(17)
areaFromDiameter(-10.2)
Experiment with this example in the TypeScript Playground.
As you can see, we can give the function any input values, as long as they are numbers. If you try to call areaFromDiameter("not a number") or areaFromDiameter(false), TypeScript will give you type errors.
Importantly, even a negative number is totally ok according to TypeScript. But a negative number obviously doesn’t make sense when we’re talking about calculating the area of a shape. This is a good reminder that while static typing is helpful, it will not prevent all kinds of errors in programming.
Function calls are expressions
When you have a function that returns a value, and you call that function with a value for its parameter, what happens?
Consider the function call
areaFromDiameter(10)
When the code above runs, the value 10 is substituted in wherever there is a reference to the diameter variable. So you can imagine that, during program execution, the function body is now:
return Math.PI * (10 / 2) * (10 / 2);
And we can go further, replacing Math.PI with a numerical value for $\pi$
return 3.14159 * (10 / 2) * (10 / 2);
And then this expression can be evaluated the same way you would in mathematics, and the value 78.53981633974483 is returned.
We can use this value because, like in math, when a function returns a value, calls to that function are also expressions. Recall our definition of expressions from last week — an expression is anything that can be evaluated to a value.
This means we can use the value returned by calls to areaFromDiameter. Returning to the “annulus” example above:
const area10: number = areaFromDiameter(10);
const area17: number = areaFromDiameter(17);
const areaAnnulus: number = area17 - area10;
In the code above, areaFromDiameter(10) is an expression that evaluates to the value 78.53981633974483.
areaFromDiameter(17) is an expression that evaluates to the value 226.98006922186258.
We can then use these values in further computation, e.g., to calculate the area of the annulus.
The entire snippet above can also be rewritten like a mathematical expression, just like we did in the beginning of this module.
const areaAnnulus: number = areaFromDiameter(17) - areaFromDiameter(10);
When the program executes, the expression areaFromDiameter(17) is replaced with the body of the areaFromDiameter function (which in turn replaces references to the diameter parameter with the value 17).
The same thing happens for the expression areaFromDiameter(10).
So you can imagine that we end up with:
const areaAnnulus: number = (Math.PI * (17 / 2) * (17 / 2)) - (Math.PI * (10 / 2) * (10 / 2));
Once all of this is done, we’re just left with one big expression. We can evaluate this using the rules of computation that you’re already used to, and produce one single value, which is given to the areaAnnulus variable.
-
The function can also not return anything, in which case its output type is
void. We won’t typically write functions that don’t return anything, but we may use such functions (e.g., those that are in-built in TypeScript). ↩